Talking to a friend, a question came up about finding the point in LA's road network that's most inconvenient to get to, with inconvenient being a vague notion describing a closed residential neighborhood full of dead ends; the furthest of these dead ends would be most inconvenient indeed. I decided to answer that question. All the code lives in a new repo: https://github.com/dkogan/culdesacs
I want inconvenient to mean
Furthest to reach via the road network, but nearest as-the-crow-flies.
Note that this type of metric is not a universal one, but is relative to a particular starting point. This makes sense, however: a location that's inconvenient from one location could be very convenient from another.
This metric could be expressed in many ways. I keep it simple, and compute a relative inefficiency coefficient:
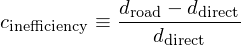
Thus the goal is to find a location within a given radius of the starting point that maximizes this relative inefficiency.
Approach
I use OpenStreetMap for the road data. This is all aimed at bicycling, so I'm looking at all roads except freeways and ones marked private. I am looking at footpaths, trails, etc.
Once I have the road network, I run Dijkstra's Algorithm to compute the shortest path from my starting point to every other point on the map. Then I can easily compute the inefficiency for each such point, and pick the point with the highest inefficiency. I use OSM nodes as the "points". It is possible that the location I'm looking for is inbetween a pair of nodes, but the nodes will really be close enough. Also, the "distance" between adjacent nodes can take into account terrain type, elevation, road type and so on. I ignore all that, and simply look at the distance.
Implementation
Each step in the process lives in its own program. This simplifies implementation and makes it easy to work on each piece separately.
Data import
First I query OSM. This is done with the query.pl script. It takes in the
center point and the query radius. The query uses the OSM Overpass query
language. I use this simple query, filling in the center point and radius:
[out:json]; way ["highway"] ["highway" !~ "motorway|motorway_link" ] ["access" !~ "private" ] ["access" !~ "no" ] (around:$rad,$lat,$lon); (._;>;); out;
Sample invocation:
$ ./query.pl --center 34.0690448,-118.292924 --rad 20miles
% Total % Received % Xferd Average Speed Time Time Time Current
Dload Upload Total Spent Left Speed
100 .....
$ ls -lhrt *(om[1])
-rw-r--r-- 1 dima dima 81M Aug 14 00:44 query_34.0690448_-118.292924_20miles.json
Data massaging
Now I need to take the OSM query results, and manipulate them into a form
readable by the Dijkstra's algorithm solver. This is done by the
massage_input.pl script. This script does nothing interesting, but it doesn it
inefficiently, so it's CPU and RAM-hungry and takes a few minutes. Sample
invocation:
$ ./massage_input.pl query_34.0690448_-118.292924_20miles.json > query_34.0690448_-118.292924_20miles.net
Neighbor list representation
An implementation choice here was how to represent the neighbor list for a node.
I want the main computation (next section) to be able to query this very
quickly, and I don't want the list to take much space, and I don't want to
fragment my memory with many small allocations. Thus I have a single contiguous
array of integers neighbor_pool. Each node has a single integer index into
this pool. At this index the neighbor_pool contains a list of node indices
that are neighbors of the node in question. A special node index of -1 signifies
the end of the neighbor list for that node.
Inefficiency coefficient computation
I now feed the massaged data to Dijkstra's algorithm implemented in compute.c.
I need a priority queue where elements can be inserted, removed and updated.
Apparently most heap implementations don't have an 'update' mechanism, so it
took a little while to find a working one. I ended up using phk's b-heap
implementation from the varnish source tree. It stores arbitrary pointers
(64-bit on my box); 32-bit indices into a pool would be more efficient, but this
is fast enough.
Sample invocation:
$ ./compute < query_34.0690448_-118.292924_20miles.net > query_34.0690448_-118.292924_20miles.out $ head -n 2 query_34.0690448_-118.292924_20miles.out 34.069046 -118.292923 0.000000 0.000000 34.070034 -118.292931 109.863564 109.863564
The output is all nodes, sorted by the road distance to the node. The columns are lat,lon,droad,ddirect.
Distance from latitude/longitude pairs
One implementation note here is how to compute the distance between two latitude/longitude pairs. The most direct way is to convert each latitude/longitude pair into a unit vector, compute the dot product, take the arccos and multiply by the radius of the Earth. This requires 9 trigonometric operations and relies on the arccos of a number close to 1, which is inaccurate. One could instead compute the arcsin of the magnitude of the cross-product, but this requires even more computation. I want something simpler:

This is nice and simple. Is it sufficiently accurate? This python script tests it:
import numpy as np lat0,lon0 = 34.0690448,-118.292924 # 3rd/New Hampshire lat1,lon1 = 33.93,-118.4314 # LAX lat0,lon0,lat1,lon1 = [x * np.pi/180.0 for x in lat0,lon0,lat1,lon1] Rearth = 6371000 v0 = np.array((np.cos(lat0)*np.cos(lon0), np.cos(lat0)*np.sin(lon0),np.sin(lat0))) v1 = np.array((np.cos(lat1)*np.cos(lon1), np.cos(lat1)*np.sin(lon1),np.sin(lat1))) dist_accurate = np.sqrt( (lat0-lat1)**2 + (lon0-lon1)**2 * np.cos(lat0)*np.cos(lat1) ) * Rearth dist_approx = np.arccos(np.inner(v0,v1)) * Rearth print dist_accurate print dist_approx print dist_accurate - dist_approx
Between Koreatown and LAX there's quite a bit of difference in both latitude and longitude. Both methods say the distance is about 20km, with a disagreement of 3mm. This is plenty good enough.
Results
I want to find the least convenient location from the intersection of New Hampshire and 3rd street in Los Angeles within 20 miles or so.
All the inconvenience coefficients computed from this data look like this (source, data):
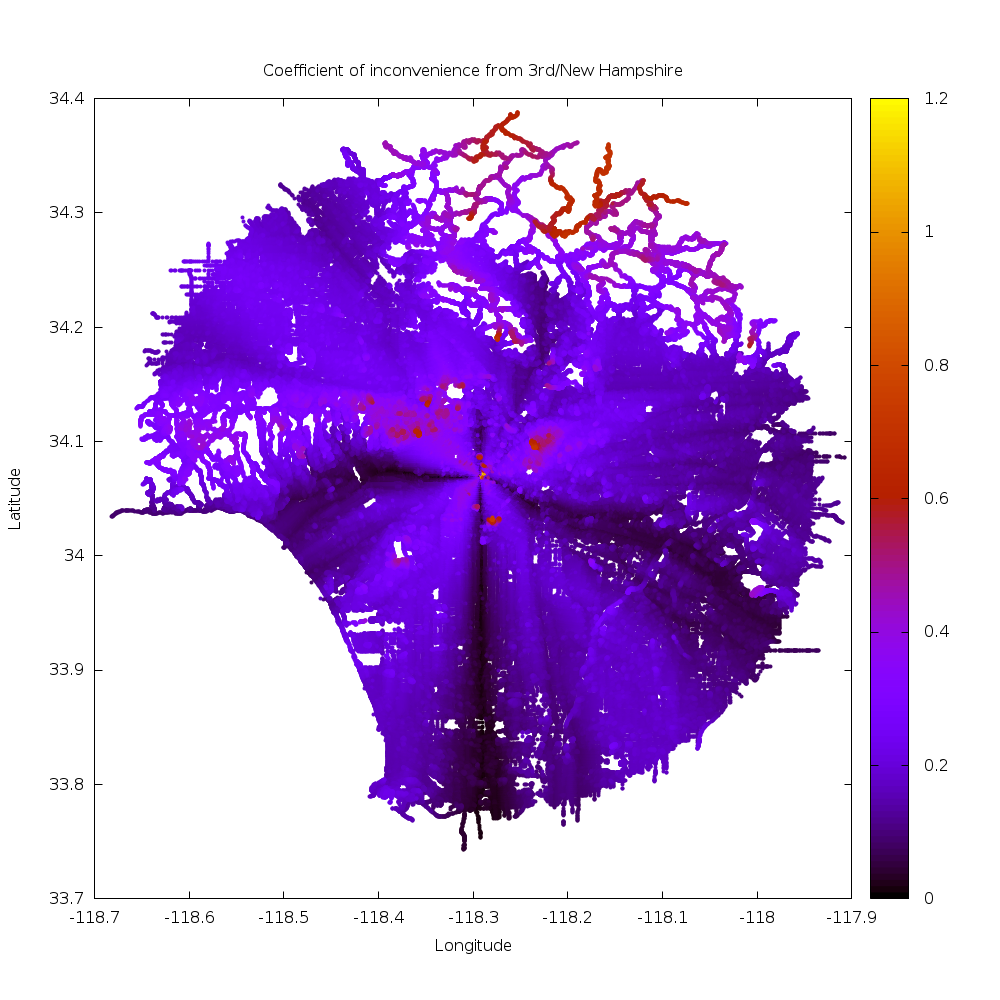
As expected, straight roads away from the starting point are highly efficient, and we see this in the Vermont corridor, 3rd street, and to a lesser extent 6th street going East. Also as expected, routes that do not align with the street grid are inefficient: we see inefficiency bumps going NW and SW from the starting point. Eastward from the start the street grid tilts, so things are more complicated in that direction.
We also see that hilly neighborhoods stand out: winding streets are not efficient. The Santa Monica mountains, Verdugos, Mount Washington and the San Gabriel Mountains clearly stand out. One can also make out the river paths in the bottom-right as ridges of inconvenience: their limited access nature makes it necessary to travel longer distance to get to them.
Onwards. The output of compute is sorted by road distance from the start. I
prepend the coefficient of inconvenience, re-sort the list and take 50 most
inconvenient locations by invoking
$ <query_34.0690448_-118.292924_20miles.out
awk '$4 {printf "%f %f %f %f %f\n",($3-$4)/$4,$1,$2,$3,$4}' |
sort -n -k1 -r | head -n 50
The output is this:
| Inconvenience | Latitude | Longitude | Road distance (m) | Direct distance (m) |
|---|---|---|---|---|
| 1.142052 | 34.068104 | -118.290382 | 549.216980 | 256.397583 |
| 1.139839 | 34.071629 | -118.288956 | 994.499390 | 464.754242 |
| 1.139147 | 34.068066 | -118.290436 | 542.721497 | 253.709305 |
| 1.136799 | 34.068130 | -118.290329 | 554.962891 | 259.716919 |
| 1.127631 | 34.068031 | -118.290466 | 537.980652 | 252.854279 |
| 1.120537 | 34.068153 | -118.290253 | 562.437012 | 265.233337 |
| 1.106771 | 34.067982 | -118.290504 | 531.442017 | 252.254257 |
| 1.103518 | 34.068169 | -118.290184 | 568.985352 | 270.492218 |
| 1.083344 | 34.067940 | -118.290527 | 526.321899 | 252.633179 |
| 1.079027 | 34.068176 | -118.290100 | 576.762024 | 277.419189 |
| 1.041816 | 34.067883 | -118.290543 | 519.805908 | 254.580200 |
| 1.034252 | 34.070259 | -118.291237 | 418.454498 | 205.704315 |
| 1.019096 | 34.071594 | -118.287888 | 1097.392212 | 543.506653 |
| 0.974731 | 34.068214 | -118.289680 | 617.407532 | 312.654022 |
| 0.970095 | 34.068176 | -118.289719 | 611.899475 | 310.593842 |
| 0.917598 | 34.068111 | -118.289383 | 656.267517 | 342.234131 |
| 0.910048 | 34.068165 | -118.289383 | 650.329041 | 340.477783 |
| 0.902491 | 34.068214 | -118.289383 | 644.814758 | 338.931915 |
| 0.770809 | 34.067570 | -118.290543 | 485.023560 | 273.899414 |
| 0.760711 | 34.068214 | -118.288643 | 712.981384 | 404.939484 |
| 0.753344 | 34.068214 | -118.288597 | 717.197876 | 409.045654 |
| 0.750541 | 34.033188 | -118.279716 | 7297.569824 | 4168.751465 |
| 0.747349 | 34.031826 | -118.279968 | 7526.415039 | 4307.333008 |
| 0.743357 | 34.067772 | -118.289474 | 606.347107 | 347.804382 |
| 0.741902 | 34.067787 | -118.289436 | 610.249084 | 350.334900 |
| 0.740024 | 34.067749 | -118.289505 | 602.555115 | 346.291290 |
| 0.739944 | 34.031769 | -118.279823 | 7511.619141 | 4317.161621 |
| 0.738388 | 34.031582 | -118.280746 | 7499.802734 | 4314.228516 |
| 0.737889 | 34.067795 | -118.289398 | 613.863831 | 353.223755 |
| 0.737716 | 34.031742 | -118.279800 | 7507.977051 | 4320.601562 |
| 0.736297 | 34.031372 | -118.280258 | 7550.486816 | 4348.613770 |
| 0.735083 | 34.068108 | -118.288734 | 693.459473 | 399.669403 |
| 0.734607 | 34.067730 | -118.289520 | 600.010803 | 345.905945 |
| 0.732851 | 34.031685 | -118.279747 | 7499.933105 | 4328.088379 |
| 0.730817 | 34.067795 | -118.289352 | 618.080322 | 357.103241 |
| 0.730543 | 34.031654 | -118.279732 | 7496.259766 | 4331.739746 |
| 0.728622 | 34.031628 | -118.279724 | 7493.208496 | 4334.787109 |
| 0.727123 | 34.067707 | -118.289536 | 597.103455 | 345.721344 |
| 0.726802 | 34.031601 | -118.279724 | 7490.239258 | 4337.637207 |
| 0.724309 | 34.031563 | -118.279739 | 7485.770508 | 4341.315430 |
| 0.723138 | 34.067791 | -118.289307 | 622.318115 | 361.153992 |
| 0.722826 | 34.031540 | -118.279755 | 7482.862793 | 4343.366211 |
| 0.722384 | 34.094849 | -118.236145 | 10273.032227 | 5964.425293 |
| 0.721979 | 34.094719 | -118.235779 | 10309.708008 | 5987.128906 |
| 0.721011 | 34.094639 | -118.235474 | 10339.187500 | 6007.625977 |
| 0.720812 | 34.094620 | -118.235405 | 10345.856445 | 6012.193359 |
| 0.720105 | 34.031498 | -118.279778 | 7477.742188 | 4347.258789 |
| 0.720078 | 34.094543 | -118.235138 | 10371.867188 | 6029.880859 |
| 0.719789 | 34.031509 | -118.279755 | 7475.278809 | 4346.624512 |
| 0.719616 | 34.095020 | -118.236320 | 10248.023438 | 5959.484863 |
There are 3 clusters of data. All the stuff < 500m away from the start is mostly degenerate and uninteresting (source):
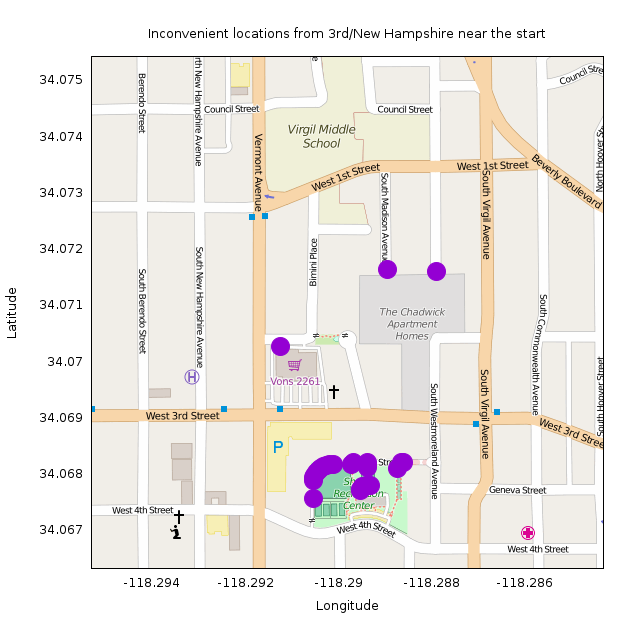
Most of the points are in walkways in Shatto Recreation Center. They're all so close to the start that any inefficiency is exaggerated by the small direct distance. I make the rules, so I claim these aren't the least convenient point.
Next we have the points about 4.2km away as the crow flies (source):
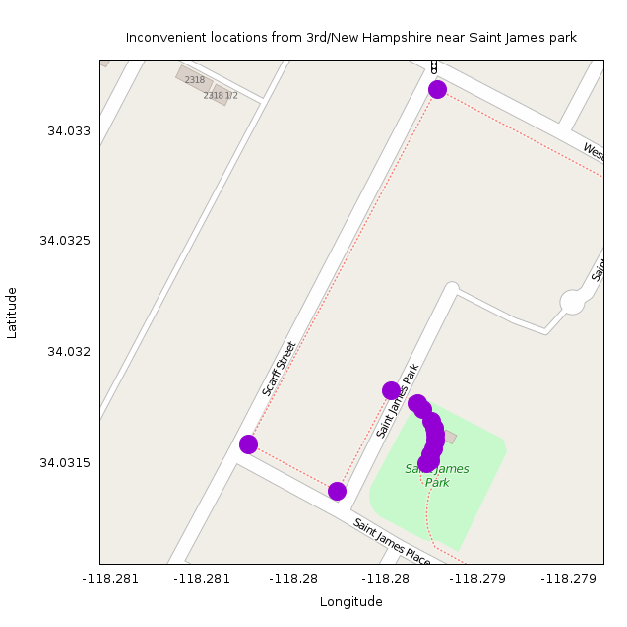
These all appear in an improperly-mapped group of sidewalks around Saint James park: http://www.openstreetmap.org/#map=18/34.03173/-118.27892.
Here the sidewalks appear as separate ways that don't connect with the roads they abut. So according to the data, connecting to the network of sidewalks can only happen in one location, making these appear less convenient than they actually are. (I think these should be removed from OSM, but it looks like the OSM committee people think that mapping sidewalks as separate ways is acceptable. OK; it'll be fixed eventually in some way).
The next cluster of data is about 6km away as the crow flies (source):
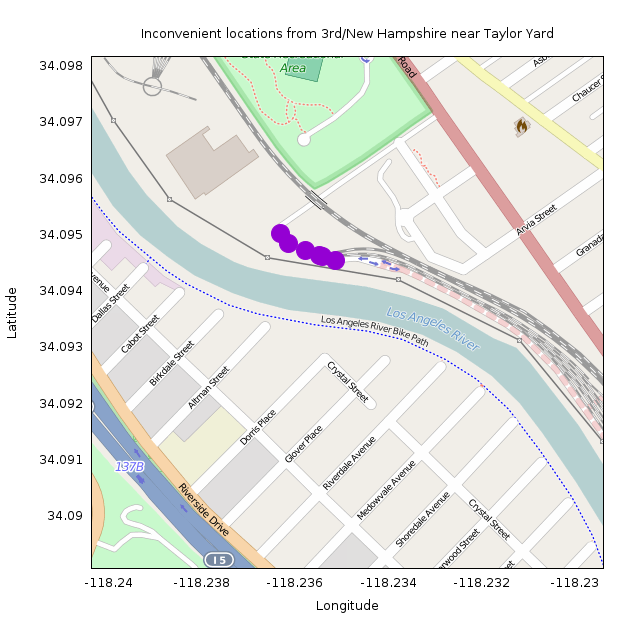
These are all at the road connecting to the Metrolink maintenance facility at Taylor Yard: http://www.openstreetmap.org/#map=17/34.09371/-118.23463. This makes sense! This location is on the other side of the LA river from Koreatown, so getting here requires a lengthy detour to the nearest bikeable bridge. The nearest one (Riverside Drive) is 2.5km by road away, but this is in the opposite direction from Koreatown. The nearest one in the other direction is Fletcher Drive, 3.8km by road.
So the least convenient point from New Hampshire / 3rd is at lat/lon 34.094849,-118.236145. This location is 10.3km away by road, but only 6.0km as the crow flies, for an inconvenience coefficient of 0.72.